求抽象函数高阶导数(第一百五十六夜)
没错,又是导数结合抽象函数,经常考,所以经常选。司空见惯、层出不穷的试题,想必你亦是无法熟视无睹吧?
那,怎么破呢?
像这样的试题,看似花里胡哨,实则不堪一击,无非是借助单调性一招破解。
你恐怕是误会了,我说的是怎么破解这种雷打不动的镇定。
呃……吃火锅去。
好的,马上。
成功已破。


题目没有太多新意,还是熟悉的配方,还是熟悉的味道。
首先根据题设判断函数的单调性,继而利用单调性构建不等式,最后分离参数或者分类讨论即可。
2 套路:手足无措,抑或从容不迫
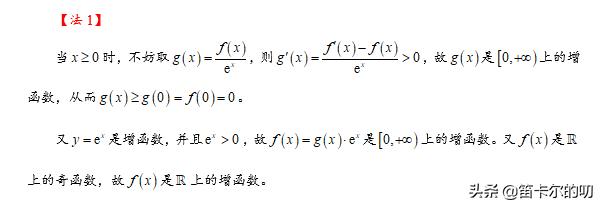
本题考导数,涉及函数的奇偶性、单调性、导数的运算、不等式的解法等知识点,综合考查函数与方程、不等式的思想、转化与划归的思想,属于难题。
法1,通过导数模型构造辅助函数,通过辅助函数的单调性得到原函数的单调性,进而得到含参不等式。
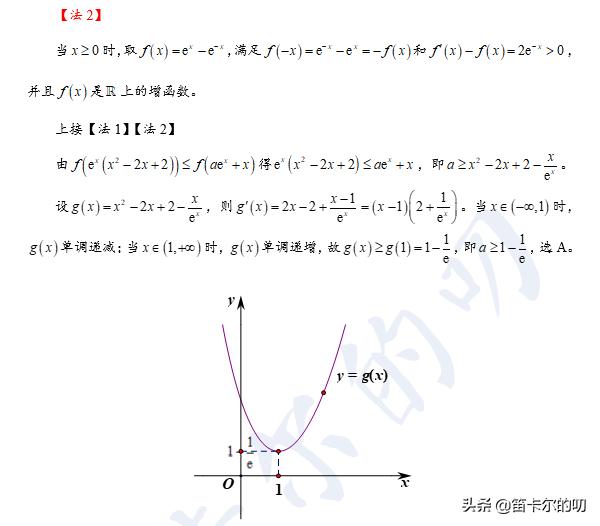
法2,通过观察找到特殊的函数模型满足题设,利用特殊函数的单调性得到不等式。
值得说明的是,两个单调函数的乘积并没有确切的单调性,需要结合二者函数值的正负进行综合判断。另外,法2中所构造的函数不易想到,事实上这是双曲正弦函数的两倍。
不知道为什么,总有一些不登大雅之堂的想法冒出来,权当笑谈吧。



夜,那么长,以数学疗人寂寞,不是修行,就是罪过。
叨叨
2019.11.11
,免责声明:本文仅代表文章作者的个人观点,与本站无关。其原创性、真实性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容文字的真实性、完整性和原创性本站不作任何保证或承诺,请读者仅作参考,并自行核实相关内容。






