第二次函数压轴题解题方法(郑州一模填空压轴题惊现双曲余弦函数)
上一篇我们说的是郑州一模的导数压轴大题,今天我们来看一下填空中的导数压轴,那可是出现了双曲余弦函数的影子,在求导的过程中。

16·已知函数f(x)=e²ˣ-e⁻²ˣ-ax,若f(x)有两个不同的极值点x₁、x₂,且0<x₂-x₁<㏑2,则a的取值范围为____。
分析:
本题难的不是函数f(x)=e²ˣ-e⁻²ˣ-ax的复杂程度,而是“f(x)有两个不同的极值点x₁、x₂”这句话,让很多人走上了极值点偏移的不归路,其实不是,若有f(x₁)=f(x₂)的便是!
事实上,“f(x)有两个不同的极值点x₁、x₂”,这句话的意思是告诉我们,函数f(x)的导函数有两个不同的零点,仍然是零点问题。
可喜的是,在对f(x)的求导过程中,惊现了双曲余弦函数的影子!
有fˊ(x)=2e²ˣ+2e⁻²ˣ-a,令其为0,
则有e²ˣ+e⁻²ˣ=a/2。
若g(x)=e²ˣ+e⁻²ˣ,(g(x)/2就是双曲余弦函数),即g(x)=a/2。
此时,风向变了,问题可以转化为,直线y=a/2与函数g(x)相交且有两个不同的交点,即g(x₁)=g(x₂)。
还是对g(x)=e²ˣ+e⁻²ˣ求个导吧!
易知,gˊ(x)=2e²ˣ-2e⁻²ˣ,
显然,gˊ(0)=0,从而g(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增。
又g(0)=2,故g(x)的图象大致如下:
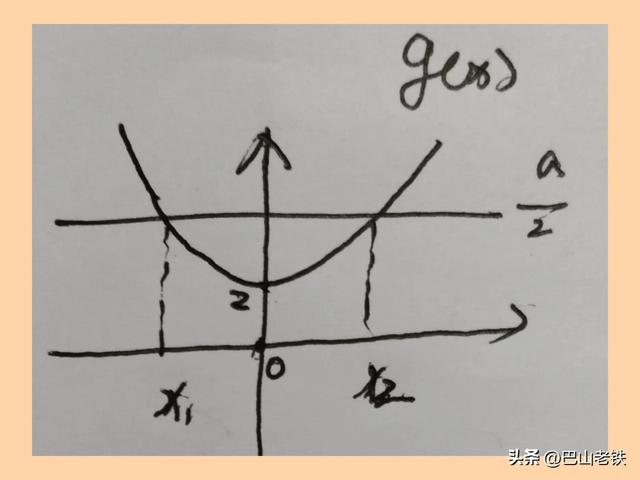
所以,有
g(x₁)=e²ˣ¹+e⁻²ˣ¹=a/2 ……①
g(x₂)=e²ˣ²+e⁻²ˣ²=a/2 ……②
①、②可联立方程组,对这个方程组的处理是有些技巧的,目的就是消参,化繁为简的!
①÷②,(左÷左,右÷右),化简后得
e²ˣ¹+e⁻²ˣ¹=e²ˣ²+e⁻²ˣ²,
e²ˣ¹-e²ˣ²=e⁻²ˣ²-e⁻²ˣ¹,
利用平方差公式来进一步优化,得
(eˣ¹+eˣ²)(eˣ¹-eˣ²)=(e⁻ˣ²+e⁻ˣ¹)(e⁻ˣ²-e⁻ˣ¹),
(eˣ¹+eˣ²)(eˣ¹-eˣ²)=(1/eˣ²+1/eˣ¹)(1/eˣ²-1/eˣ¹),
右边各自通分后再化简,得
(eˣ¹eˣ²)²=1,即eˣ¹eˣ²=1,
故有x₁+x₂=0,即x₁=-x₂。
结合已知条件:0<x₂-x₁<㏑2,有
0<2x₂<㏑2,即0<x₂<㏑2/2。
因此,有g(0)=2,g(㏑2/2)=5/2,
则有g(0)<g(x₂)<g(㏑2/2),
即2<a/2<5/2,
故4<a<5。
这就是整个解题思路,是不是有点不可思议呢,既化参的又消元的?
有没有更简单的方法呢?






是的,的确如此!
因为,这道题是做为填空题的,尽管压轴,也绝不会这般繁杂,一定会有更简单的。
事实上,该问题等价于导函数有两个不同的零点,因导函数是偶函数,有x₁=-x₂,数形结合,求临界情况时的a值即可。
是不是要妙杀呢?
,免责声明:本文仅代表文章作者的个人观点,与本站无关。其原创性、真实性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容文字的真实性、完整性和原创性本站不作任何保证或承诺,请读者仅作参考,并自行核实相关内容。






